<FONT FACE=“Courier New”>
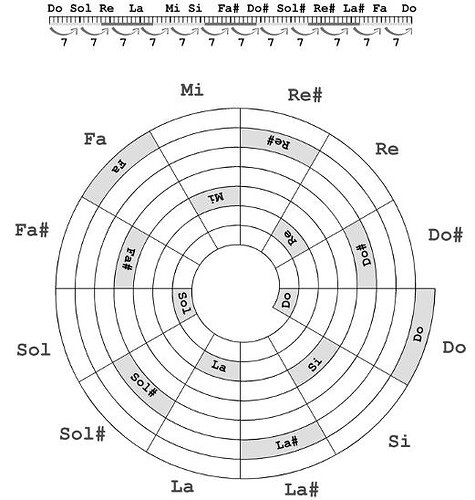
Αφού σας αρέσουν αυτά τα κουκιδάκια και τις τροχαλίες, πάρτε μιά πρώτη γεύση από το πως σχηματίζεται ο παραπάνω τροχός ΣΩΣΤΑ και χωρίς διάφωνα διαστήματα.
Εχουμε και λέμε:
Ο Πυθαγόρας, από τον 6ο αιώνα π.Χ ανακάλυψε πως το διάστημα της καθαρής πέμπτης, που αντιστοιχεί σε λόγο συχνοτήτων 3/2, μαζί με το διάστημα πλήρους οκτάβας 2/1, είναι ιδιαίτερα σύμφωνα. Από αυτή τη θεμελιώδη παρατήρηση συμπέρανε πως η μουσική κλίμακα οφείλει να σχηματίζεται με χρήση του κλάσματος της καθαρής πέμπτης 3/2 και του κλάσματος της πλήρους οκτάβας 2/1.
Η διαδικασία
Ας σχηματίσουμε την κλίμακα Fa - Sol - La - Si - Do - Re - Mi - Fa’
Ο πρώτος φθόγγος είναι ο Fa που βρίσκεται σε ταυτοφωνία με τον εαυτό του. Δηλαδή σε σχέση 1/1. Για την πληρότητα της κλίμακας χρειαζόμαστε και τον Fa’ μια οκτάβα πάνω από τον αρχικό Fa. Επειδή, όπως θα δούμε, όσες πέμπτες και να προσθέσουμε δεν θα πάρουμε ποτέ μια πλήρη οκτάβα (2/1), ορίζουμε την οκτάβα με λόγο 2/1.
Fa Fa# Sol Sol# La La# Si Do Do# Re Re# Mi Fa’
1/1 2/1
Εισάγουμε τον επόμενο φθόγγο Do σε απόσταση καθαρής πέμπτης από τον Fa, δηλ. σε σχέση 3/2
Fa Fa# Sol Sol# La La# Si Do Do# Re Re# Mi Fa’
1/1 3/2 2/1
Για τον τρίτο φθόγγο Sol πρέπει να προσθέσουμε στο Do άλλη μία καθαρή πέμπτη (3/2). Στη κλασματική κλίμακα αυτό σημαίνει να πολλαπλασιάσουμε το (3/2) επί το (3/2). Μια καθαρή πέμπτη πάνω από τον Do θα έδινε τον Sol’ που απέχει μια μεγάλη ενάτη (14 ημιτόνια) από τον αρχικό Fa. H σχέση που θα είχαν είναι (3/2) x (3/2) = 9/4. Όμως είναι εκτός οκτάβας Fa - Fa’, οπότε παίρνουμε το μισό του (9/4) : (1/2) = 9/8 που είναι και αυτός Sol αλλά μέσα στα όρια της κλίμακάς μας. Λέγοντας “παίρνουμε το μισό του”, ουσιαστικά σημαίνει “αφαιρώ μία οκτάβα”.
Fa Fa# Sol Sol# La La# Si Do Do# Re Re# Mi Fa
1/1 9/8 3/2 2/1
Ως εδώ μάθαμε ότι
για να αθροίσουμε δύο διαστήματα πολλαπλασιάζουμε τους λόγους τους,
για να αφαιρέσουμε δύο διαστήματα διαιρούμε τους λόγους τους.
Επιπλέον, διαπιστώνουμε πως
A. το διάστημα μιας τετάρτης (Sol - Do) είναι ίσο με τη διαφορά του Do μείον τον Sol, δηλ. (3/2):(9/8) = 4/3
B. το διάστημα μιας μεγάλης δευτέρας (Fa - Sol) είναι ίσο με τη διαφορά το Sol μείον τον Fa, δηλ. (9/8):(1/1) = 9/8
Η συνέχεια είναι εύκολη και οι πράξεις δίνονται συνοπτικά:
Fa = 1/1
Do = Fa + (3/2) = (1/1)x(3/2) = 3/2
Sol = Do + (3/2) = (3/2)x(3/2) = 9/4 > 2/1 άρα αφαιρώ 2/1. Έτσι (9/4):(2/1) = 9/8
Re = Sol + (3/2) = (9/8)x(3/2) = 27/16
La = Re + (3/2) = (27/16)x(3/2) = 81/32 > 2/1 άρα (81/32):(2/1) = 81/64
Mi = La + (3/2) = (81/64)x(3/2) = 243/128
Si = Mi + (3/2) = (243/128)x(3/2) = 729/256 > 2/1 άρα (729/256):(2/1)=729/512
Όσα ξέραμε μέχρι και την εύρεση του Sol αρκούσαν για την εύρεση όλων των υπολοίπων φθόγγων της κλίμακας. Για να βρούμε τον La αρκεί να προσθέσουμε ένα διάστημα μεγάλης δευτέρας 9/8 (Πυθαγόρειος Μείζων Τόνος) στο Sol. Μετά, για να βρούμε τον Si αρκεί να προσθέσουμε ένα διάστημα μεγάλης δευτέρας στον Sol που βρήκαμε πριν κ.ο.κ.
La = Sol + (9/8) = (9/8)x(9/8) = 81/64
Si = La + (9/8) = (81/64)x(9/8) = 729/512
Re = Do + (9/8) = (3/2)x(9/8) = 27/16
Mi = Re + (9/8) = (27/16)x(9/8) = 243/128
Τελικά:
Fa Fa# Sol Sol# La La# Si Do Do# Re Re# Mi Fa’
1/1 9/8 81/64 729/512 3/2 27/16 243/128 2/1
Τα διαστήματα Si-Do και Mi-Fa’ είναι ίσα με το Έλασσον Ημιτόνιο = 256/243 ή 28 / 35
αφού Do μείον Si = (3/2):(729/512) = (2/1):(243/128)= 256/243 αλλά και Fa’ μείον Mi = (2/1):(243/128)= 256/243
Τα υπόλοιπα διαστήματα είναι όλα ίσα με τον Μείζονα Τόνο = 9/8 ή 32/23
Τα ημιτόνια δεν είναι το μισό του τόνου: To Do συν Έλασσον Ημιτόνιο = (3/2)x(256/243) = 128/81 και Re μείον Έλασσον Ημιτόνιο 256/243 = (27/16):(256/243) = 6541/4096. Όφειλαν να είναι ίσα, αλλά έχουν διαφορά ίση με (6541/4096):(128/81)=25567/25300
Η απόσταση Do# - Si είναι Do# = (128/81):(729/512) = 65536/59049 = 216/310
Δηλαδή δύο ημιτόνια δίνουν λόγο συχνοτήτων 216/310 αντί για 9/8. Αυτό ισοδυναμεί με διαφορά
(216/310):(9/8)= (216/310)
32/24)= 219/312 που είναι περίπου ίσο με το 1 (δηλαδή η απόσταση εκμηδενίζεται).
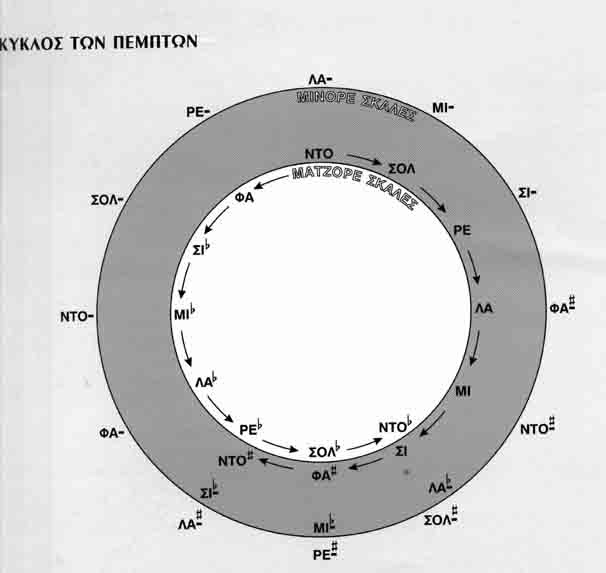
Με λίγα λόγια, το πυθαγόρειο σύστημα βασίζεται στο ότι 219≈312, ή 524288 ≈531441. Έτσι, ανεβαίνοντας από ένα φθόγγο 12 πέμπτες (12x7=84 ημιτόνια) και κατεβαίνοντας 7 οκτάβες (7x12 = 84 ημιτόνια) επιστρέφεις περίπου στον αρχικό φθόγγο. Από το γεγονός ότι δεν ταυτίζονται, εμφανίζεται η ανάγκη του ορισμού του Πυθαγόρειου κόμματος: 312/219 = 1.013643265, κάτι περισσότερο από το ένα ένατο του τόνου.
ΟΡΟΛΟΓΙΑ
Μία οκτάβα (2/1) μείον μία καθαρή πέμπτη (3/2) κάνει μία καθαρή τετάρτη (4/3).
Μία καθαρή πέμπτη (3/2) μείον μια καθαρή τετάρτη (4/3) κάνει ένα Πυθαγόρειο Μείζονα τόνο (9/8).
Μία καθαρή τετάρτη (4/3) μείον δύο τόνους (18/8) κάνει ένα Πυθαγόρειο έλασσον ημιτόνιο (256/243). Αρχικά λεγόταν δίεση (εκ του “διαφορά”) και αργότερα λήμμα.
Ένας τόνος (9/8) μείον μία δίεση (256/243) κάνει ένα Πυθαγόρειο Μείζον Ημιτόνιο (2187/2048) που λέγεται και αποτομή.
Μία αποτομή (2187/2048) μείον μία δίεση (256/243) κάνει ένα Πυθαγόρειο κόμμα (531441/524288).
Ενδιαφέρον για τον μελετητή παρουσιάζει και ο πίνακας που ακολουθεί. Η στήλη “διόρθωση” αφορά την απλή πράξη της επαναφοράς του φθόγγου που ξεφεύγει από τα όρια της οκτάβας Fa - Fa’ με αφαίρεση μιας οκτάβας (2/1), που στην διαστηματική λογική σημαίνει διαίρεση με το ίδιο κλάσμα:
προηγούμενος φθόγγος + μια 5η = διόρθωση φθόγγος κλίμακα
ορισμός: 1/1 Fa
1/1 3/2 3/2 όχι 3/2 Do
3/2 3/2 9/4 :(2/1) 9/8 Sol
9/8 3/2 27/16 όχι 27/16 Re
27/16 3/2 81/32 :(2/1) 81/64 La
81/64 3/2 243/128 όχι 243/128 Mi
243/128 3/2 729/256 :(2/1) 729/512 Ti
729/512 3/2 2187/1024 :(2/1) 2187/2048 Fa#
2187/2048 3/2 6561/4096 όχι 6561/4096 Do#
6561/4096 3/2 19683/8192 :(2/1) 19683/16384 Sol#
19683/16384 3/2 59049/32768 όχι 59049/32768 Re#
59049/32768 3/2 177147/65536 :(2/1) 177147/131072 La#
177147/131072 3/2 531441/262144 :(2/1) 531441/524288* Fa’
Τα επόμενα κεφάλαια έχουν πολλά σχήματα (κι αυτό είχε αλλά τα “έκοψα” για να μπορεί να βγει στο forum).
Μέσα στο καλοκαίρι ευελπιστώ να ανεβάσω ένα site με όλα τούτα τα τσιτσιμπλόνια.
(μάλλον δεν θα βγούν καλά οι πίνακες, οπότε όποιος θέλει να του στείλω ένα html ή doc ας μου το ζητήσει με mail)
</FONT>
